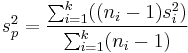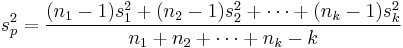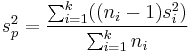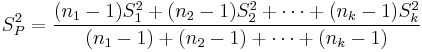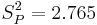Pooled variance

In statistics, many times, data are collected for a dependent variable, y, over a range of values for the independent variable, x. For example, the observation of fuel consumption might be studied as a function of engine speed while the engine load is held constant. If, in order to achieve a small variance in y, numerous repeated tests are required at each value of x, the expense of testing may become prohibitive. Reasonable estimates of variance can be determined by using the principle of pooled variance after repeating each test at a particular x only a few times. Pooled variance is a method for estimating variance given several different samples taken in different circumstances where the mean may vary between samples but the true variance (equivalently, precision) is assumed to remain the same. It is calculated by

$s_p^2=\frac{\sum_{i=1}^k((n_i - 1)s_i^2)}{\sum_{i=1}^k(n_i - 1)}$

or with simpler notation,

$s_p^2=\frac{(n_1 - 1)s_1^2%2B(n_2 - 1)s_2^2%2B\cdots%2B(n_k - 1)s_k^2}{n_1%2Bn_2%2B\cdots%2Bn_k - k}$

where s_p² is the pooled variance, n_i is the sample size of the i'th sample, s_i² is the variance of the ith sample, and k is the number of samples being combined. n − 1 is used instead of n for the same reason it may be used in estimating variances from samples (i.e. Bessel's correction).

The square-root of a pooled variance estimator is known as a pooled standard deviation.

1 Unbiased least square estimate vs. biased maximum likelihood estimate
2 Example
3 See also
4 References
5 External links

Unbiased least square estimate vs. biased maximum likelihood estimate

Both

$s_p^2=\frac{\sum_{i=1}^k((n_i - 1)s_i^2)}{\sum_{i=1}^k(n_i - 1)}$

and

$s_p^2=\frac{\sum_{i=1}^k((n_i - 1)s_i^2)}{\sum_{i=1}^k n_i }$

are used in different contexts. The former can give an unbiased 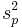$s_p^2$ to estimate 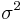$\sigma^2$ when the two groups share an equal population variance. The latter one can give a more efficient 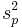$s_p^2$ to estimate 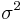$\sigma^2$ biasedly. Note that the quantities 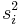$s_i^2$ in the right hand sides of both equations are the unbiased estimates.

Example

Consider the following set of data for y obtained at various levels of the independent variable x.

x	y
1	31, 30, 29
2	42, 41, 40, 39
3	31, 28
4	23, 22, 21, 19, 18
5	21, 20, 19, 18,17

The number of trials, mean, variance and standard deviation are presented in the next table.

x	n	y_mean	S_y²	S
1	3	30.0	1.0	1.0
2	4	40.5	1.67	1.29
3	2	29.5	4.5	2.12
4	5	20.6	4.3	2.07
5	5	19.0	2.5	1.58

These statistics represent the variance and standard deviation for each subset of data at the various levels of x. If we can assume that the same phenomena are generating random error at every level of x, the above data can be “pooled” to express a single estimate of variance and standard deviation. In a sense, this suggests finding a mean variance or standard deviation among the five results above. This mean variance is calculated by weighting the individual values with the size of the subset for each level of x. Thus, the pooled variance is defined by

$S_P^2 = \frac{(n_1-1)S_1^2%2B(n_2-1)S_2^2 %2B \cdots %2B (n_k - 1)S_k^2}{(n_1 - 1) %2B (n_2 - 1) %2B \cdots %2B(n_k - 1)}$

where n₁, n₂, . . . n_k are the sizes of the data subsets at each level of the variable x, and S₁², S₂², . . ., S_k² are their respective variances.

The pooled variance of the data shown above is therefore:

$S_P^2 = 2.765 \,$

References

Killeen PR (May 2005). "An alternative to null-hypothesis significance tests". Psychol Sci 16 (5): 345–53. doi:10.1111/j.0956-7976.2005.01538.x. PMC 1473027. PMID 15869691. http://www.pubmedcentral.nih.gov/articlerender.fcgi?tool=pmcentrez&artid=1473027.

Pooled variance

Contents

Unbiased least square estimate vs. biased maximum likelihood estimate

Example

See also

References

External links